Spectral Clustering: Theoretical Intuition Behind the Practical Algorithm
To kick off my blog, I want to share some thoughts on spectral clustering, a graph theory-inspired clustering technique, which I recently became interested in after taking a course by Prof. Salil Vadhan on spectral graph theory. The course was quite theoretical and required a lot of work, especially for someone who just came back to school from industry and hadn’t thought about eigen-things for awhile. Nonetheless, I learned a lot and was able to brush up on some linear algebra, which is sometimes underrated among machine learning people. In fact, I was happy to find that this seemingly niche and quite theoretical area of computer science indeed has many connections to ML, e.g. MCMC sampling, recommender systems (think PageRank), iterative optimization, clustering, etc. It makes me think that ML research can only benefit from further synergies with spectral graph theory.
In this post, I focus on one spectral graph theory method that I found particularly cool – spectral clustering. This is an unsupervised learning method for separating \(N\) data points into \(K\) sensible subgroups. There are many great tutorials online on what the algorithm is and how to use it in practice, but what I want to emphasize here is why the algorithm works. From personal experience, I know that it is easy to get stuck on why spectral clustering takes certain steps, especially when papers on the subject do not give the full intuition. I hope to clarify some common sources of confusion by diving ever-so-slightly into the theory of graph Laplacians.
Basic Algorithm
The spectral clustering algorithm requires two inputs: (1) a dataset of points \(x_1, x_2, \ldots, x_N\) and (2) a distance function \(d(x, x')\) that can quantify the distance between any two points \(x\) and \(x'\) in the dataset. A very simple distance function is Euclidean distance, i.e. \(d(x, x') = ||x - x'||_2\).
The algorithm executes the following three steps:
- Construct a graph with the vertices being data points and the edge weight matrix \(\bf M\) defined by \({\bf M}(x, x') := \exp(-d(x, x')^2 / \gamma)\) for some constant hyperparameter \(\gamma\).
- Obtain the first \(K\) eigenvectors of the normalized graph Laplacian \({\bf N} := {\bf I} - {\bf D}^{-1}{\bf M}\) as a feature embedding of the data, where \(\bf D\) is the degree matrix of the graph and \(\bf I\) is the identity matrix.
- Run a standard clustering algorithm (e.g. \(K\)-Means) on the \(K\)-dimensional features to cluster the data.
The first time I saw this algorithm, I had many questions immediately popping up in my mind, e.g.:
- Why is the edge weight matrix defined as a complicated nonlinear transformation of the distance function?
- What the heck is the normalized graph Laplacian and why are we using it?
- Why are the first \(K\) eigenvectors a good feature embedding for clustering purposes? And why is this \(K\) the same value as the number of clusters we are trying to get?
It turns out that spectral graph theory provides good answers to all of these questions.
Intro to Graph Laplacians
Spectral clustering revolves around the eigenspace of the graph Laplacian, which has some very cool properties that are useful for clustering. Forgetting the data points and clustering for a second, let’s just consider an arbitrary graph with vertices and edges. For simplicity, let the graph be unweighted (i.e. edges either exist with weight 1 or don’t with weight 0).
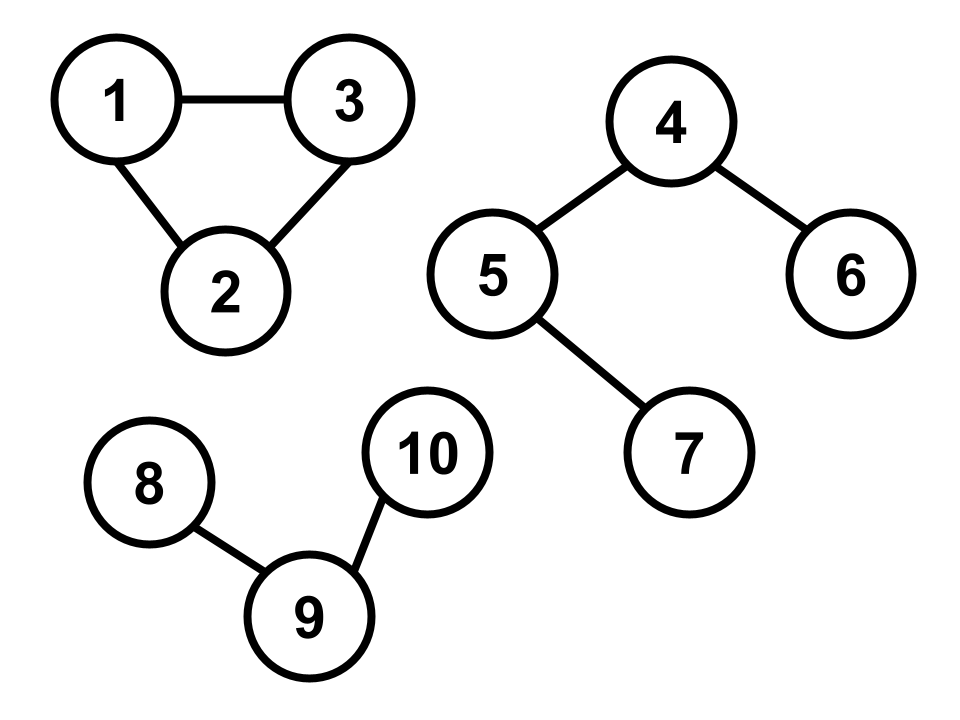 Observe that this particular graph is disconnected and can clearly be partitioned into three connected components without discarding any edges. Analyzing the Laplacian of this graph will give us a better sense of how spectral clustering works.
Assuming that each vertex is also connected to itself, the edge weight matrix \(\bf M\) and the degree matrix \(\bf D\) of this graph are
Observe that this particular graph is disconnected and can clearly be partitioned into three connected components without discarding any edges. Analyzing the Laplacian of this graph will give us a better sense of how spectral clustering works.
Assuming that each vertex is also connected to itself, the edge weight matrix \(\bf M\) and the degree matrix \(\bf D\) of this graph are
The (unnormalized) Laplacian of a graph is defined as the difference between these two matrices, i.e. \({\bf L} := {\bf D} - {\bf M}\). Now, let’s take a look at the kernel of \(\bf L\), which contains all vectors \(\bf v\) such that \(\bf L v = 0\). Consider the vector \({\bf v}_1 := \begin{bmatrix} 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\end{bmatrix}^T\), which is simply an indicator of the connected component containing vertices (1, 2, 3) in the graph depicted above. We can easily check that \({\bf L} {\bf v}_1 = \bf 0\), implying that \({\bf v}_1\) belongs to the kernel of \(\bf L\).
Next, consider an indicator of the second connected component containing vertices (4, 5, 6, 7), i.e. \({\bf v}_2 := \begin{bmatrix} 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 \end{bmatrix}^T\). Some quick arithmetic reveals that \({\bf v}_2\) also lies in the kernel \(\bf L\). Furthermore, \({\bf v}_2\) is orthogonal to \({\bf v}_1\). Finally, we can also check that an indicator of the third connected component, i.e. \({\bf v}_3 := \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1\end{bmatrix}^T\), is a third vector in the kernel of \(\bf L\) that is mutually orthogonal with both \(\mathbf{v}_1\) and \(\mathbf{v}_2\).
Indeed, these three “component indicator vectors” \(\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\) form an orthogonal basis that spans the kernel of \(\mathbf{L}\). Note that if we were to take any other indicator vector \(\mathbf{w}\) that is not a linear combination of these three, we would find that \(\mathbf{w}\) does not lie in the kernel of \(\mathbf{L}\). For example, consider \(\mathbf{w} := \begin{bmatrix} 1 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}^T\), which indicates vertices (1, 2, 4) from different connected components. We find that \(\mathbf{Lw} = \begin{bmatrix} 1 & 1 & -2 & 2 & -1 & -1 & 0 & 0 & 0 & 0 \end{bmatrix}^T\), which is clearly not the all-zeros vector \(\bf 0\).
The aforementioned example uncovers the following remarkable property of the Laplacian, which holds for any arbitrary graph:
The Laplacian matrix of a graph with \(K\) connected components has a kernel spanned by \(K\) component indicator vectors that are mutually orthogonal.
This property is central to why spectral clustering works. Recall that the first \(K\) eigenvectors of the Laplacian \(\bf{L}\) are defined as those corresponding to the smallest eigenvalues of \(\bf L\). Any vector in the kernel of a matrix is an eigenvector with eigenvalue zero. Since the graph Laplacian is positive semi-definite, all of its eigenvalues are greater than or equal to zero, which further implies that the first \(K\) eigenvectors of \(\bf L\) are exactly those in the kernel. And from the special property above, we can conclude that these first \(K\) eigenvectors are the \(K\) component indicator vectors of the graph.
From Kernel to Clustering
Now, let’s take these first \(K\) eigenvectors (\(K = 3\) in our particular case) and arrange them in a matrix:
\[\begin{bmatrix} 1 & 0 & 0\\ 1 & 0 & 0\\ 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 1 & 0\\ 0 & 1 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 1\\ 0 & 0 & 1\\ \end{bmatrix}\]This matrix has dimensions \(N \times K\) and we can think of each row \(i\) of this matrix as a feature embedding for vertex \(i\). What would happen if we threw these rows into a standard clustering algorithm like \(K\)-means to cluster the corresponding vertices? One would imagine that since the first three vertices (1, 2, 3) have identical feature embeddings, they would be clustered together. The same would go for vertices (4, 5, 6, 7) and vertices (8, 9, 10). In other words, \(K\)-means would be able to easily recover the connected components in the original graph as separate clusters!
This explains why spectral clustering seeks to find the first \(K\) eigenvectors of the graph Laplacian. As we have seen, in perfectly separable graphs, these eigenvectors serve as feature embeddings from which it is very easy for simple clustering algorithms to identify the correct clusters.
Aside: Technically, spectral clustering works with the normalized Laplacian \(\mathbf N\), defined as
\[\mathbf N := \mathbf D^{-1} \mathbf L = \mathbf I - \mathbf D^{-1} \mathbf M\]Unlike the standard Laplacian \(\mathbf L\), the normalized Laplacian’s eigenvalues are scaled so they lie within the constant range \([0, 2]\). However, this normalization by \(\mathbf D^{-1}\) does not change the kernel of the matrix, so the first \(K\) eigenvectors of \(\mathbf{N}\) still provide a good feature embedding for \(K\)-means based on the arguments above.
Generalizing to Weighted Graphs
OK, so for ideal unweighted graphs with perfectly separable connected components, spectral clustering makes sense. But how about when we work with real-world data? In those cases, we are taking data points \(x_1, x_2, \ldots, x_N\) and constructing weighted graphs based on a distance function \(d(x, x')\). Now, edges are not binary 0-1, but rather weighted by \(\exp(-d(x, x')^2 / \gamma)\), where \(\gamma\) is a predefined constant. Does our intuition for the graph Laplacian from above still hold in this more general case?
Interestingly, the answer is yes. Observe that the weight function is designed to take distances which may lie in some arbitrary range (e.g. potentially \([0, \infty)\)) and map them to \([0, 1]\). Specifically, two data points that have a large distance will have a close-to-zero weight, while two data points that have a small distance will have a close-to-one weight. Thus, instead of binary 0-1 edges, we have what looks like a soft relaxation in the range \([0, 1]\). As an example, our data may spawn a graph that looks like this:
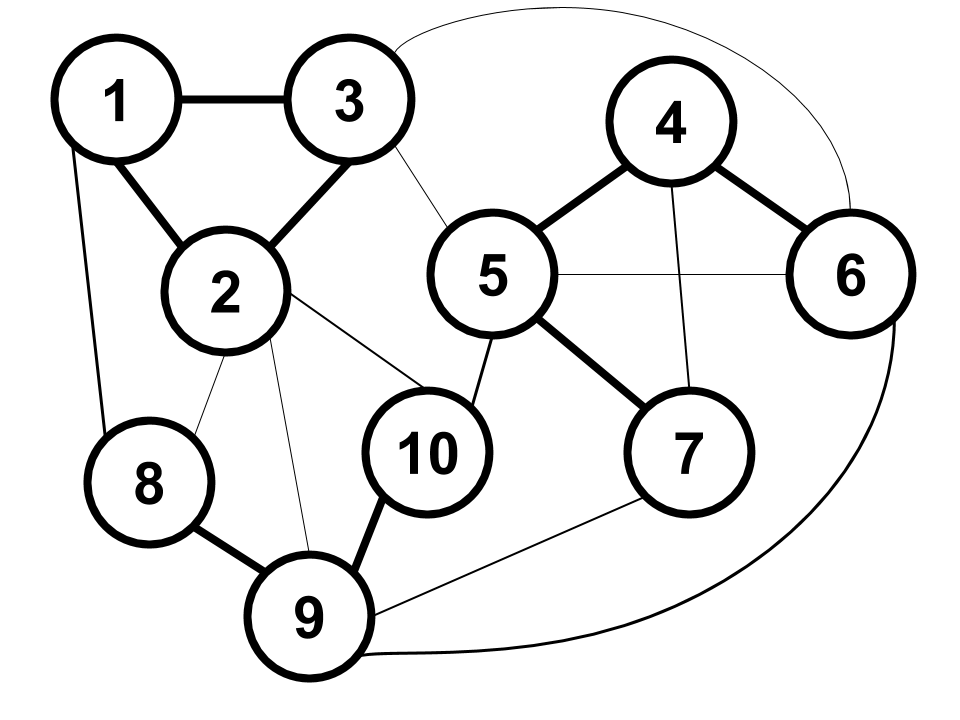 In the drawing, the weight of each edge is represented by its thickness. Technically all pairs of vertices have edges between them, but I omit some edges for ease of viewing.
In the drawing, the weight of each edge is represented by its thickness. Technically all pairs of vertices have edges between them, but I omit some edges for ease of viewing.
Compared to before, there are more edges (albeit some of them with small weight) and the entire graph is connected. As a result, there are no longer three connected components with zero edges between them. This certainly affects the eigenspace of the normalized Laplacian \(\bf N\); for example, there will be only one eigenvector (i.e. the all-ones indicator vector) in the kernel of \(\bf N\) since there is technically only one connected component (which contains the whole graph).
However, visually speaking, our weighted graph still seems to have three clear “clusters” corresponding to the connected components in the unweighted graph. In the old example, the first three eigenvalues of \(\textbf N\) were equal to zero because the three clusters had no edges between them. In our new example, it is intuitive to think that perhaps the first three eigenvalues of \(\textbf{N}\) are close to zero since there are only low-weight edges between the clusters. And indeed, this intuition can be formalized through a theorem from spectral graph theory known as higher order Cheeger’s inequality. Extending the line of thought further, the first three eigenvectors \(\mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3\) of \(\bf N\) in our new example span a subspace that is quite close to the one spanned by the three component indicator vectors \(\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3\) in our old example. Since similar inputs to \(K\)-means yields similar outputs, passing \([\mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3]\) as a feature embedding would result in a near-perfect clustering close to the one found using \([\mathbf{v}_1, \mathbf{v}_2, \mathbf{v}_3]\)!
Finally, we have arrived at the theoretical intuition behind why spectral clustering works in practice.
Answers to FAQs
Hopefully this clears up some commonly asked questions! Revisiting the list from earlier,
- Why is the edge weight matrix defined as a complicated nonlinear transformation of the distance function?
- The weight transformation \(\exp(-d(x, x')^2 / \gamma)\) creates a graph in which similar points (i.e. close in distance) have a large, close-to-one weight between them and dissimilar points (i.e. far in distance) have a small, close-to-zero weight between them. This allows us to view the resultant weighted graph as a continuous relaxation of a binary 0-1 unweighted graph, whose Laplacian has a kernel structure that is friendly for clustering.
- What the heck is the normalized graph Laplacian and why are we using it?
- The graph Laplacian is simply the difference between the degree matrix and the edge weight matrix. The normalized graph Laplacian scales the Laplacian by the inverse of the degree matrix so that all eigenvalues lie within a constant range. In cleanly separable and close-to-cleanly separable graphs, the first few eigenvectors of the Laplacian provide ideal inputs for standard clustering algorithms such as \(K\) means to work with.
- Why are the first \(K\) eigenvectors a good feature embedding for clustering purposes? And why is this \(K\) the same value as the number of clusters we are trying to get?
- In an unweighted graph with \(K\) clearly separable connected components, the first \(K\) Laplacian eigenvectors form one-hot encoded feature embeddings that are guaranteed to return a perfect clustering. This is the reason why we pass exactly \(K\) eigenvectors to \(K\)-means if we believe our data to be \(K\)-separable.
Final Thoughts
Before concluding this post, I would be remiss to not mention some of the history behind spectral clustering. Spectral clustering was first introduced to the field of machine learning through two foundational papers – Shi & Malik, 2000 and Ng, Jordan, & Weiss, 2001. Subsequently, there were a lot of works that followed on this exciting approach. In particular, von Luxburg, 2007 is a great tutorial on the subject and I highly recommend a read for those interested.
However, it seems that these days, spectral clustering has fallen slightly out of favor in parts of the machine learning community. Perhaps this is due to the high computational cost, in particular the eigendecomposition step in which we need to extract the first \(K\) eigenvectors. Yet, with recent advances in massively parallelized hardware (i.e. GPUs) and computationally efficient matrix-free solvers, I am hopeful that spectral clustering can make a comeback. If interested, check out this recent project in which I took a rudimentary crack at making spectral clustering faster using both of these ideas.